Analysis Methods

Once you load or create a network in SocNetV, you may use the options in the Analyze menu to compute graph and social network analysis measures.

---

Matrix Analysis

Options to compute, display, and analyze various matrices based on the adjacency matrix of the current network.

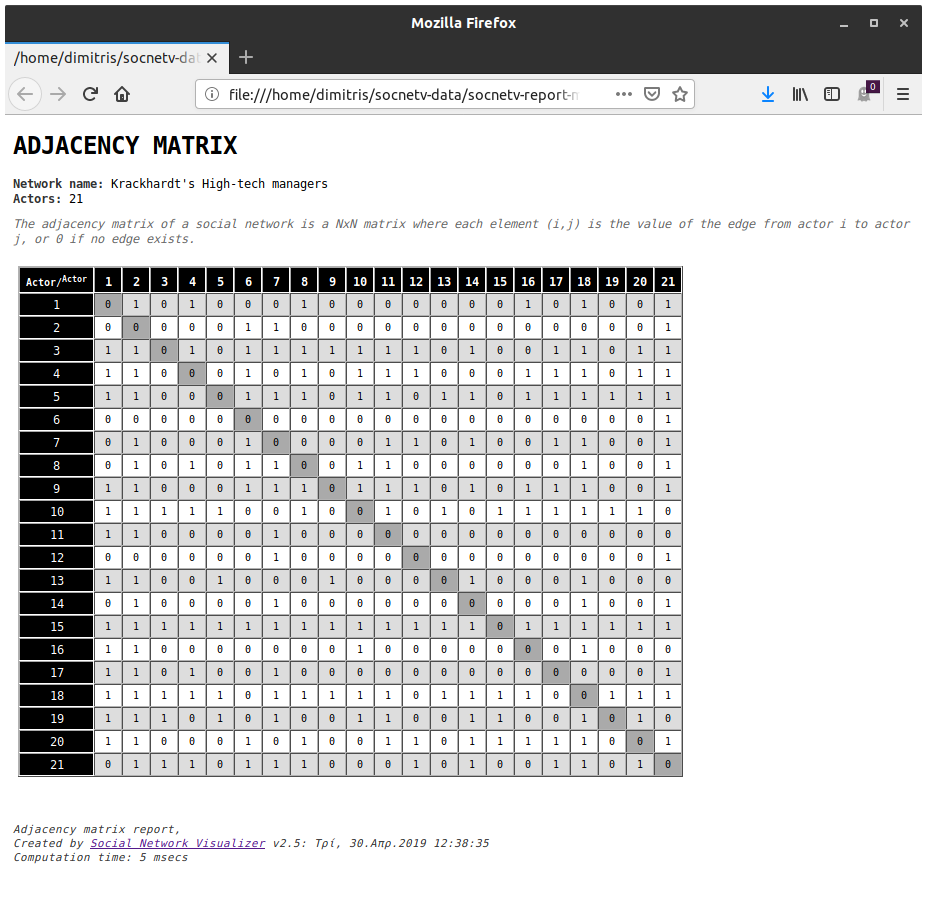
Adjacency Matrix

Displays the adjacency matrix $A$ of the active network. The matrix is displayed in HTML format in your default web browser.

The adjacency matrix of a social network is a matrix where each element $a(i,j)$ is equal to the weight of the arc from actor (node) $i$ to actor $j$. If the actors are not connected, then $a(i,j) = 0$.

---

Inverse Adjacency

This option computes the inverse $A^{-1}$ of the adjacency matrix.

---

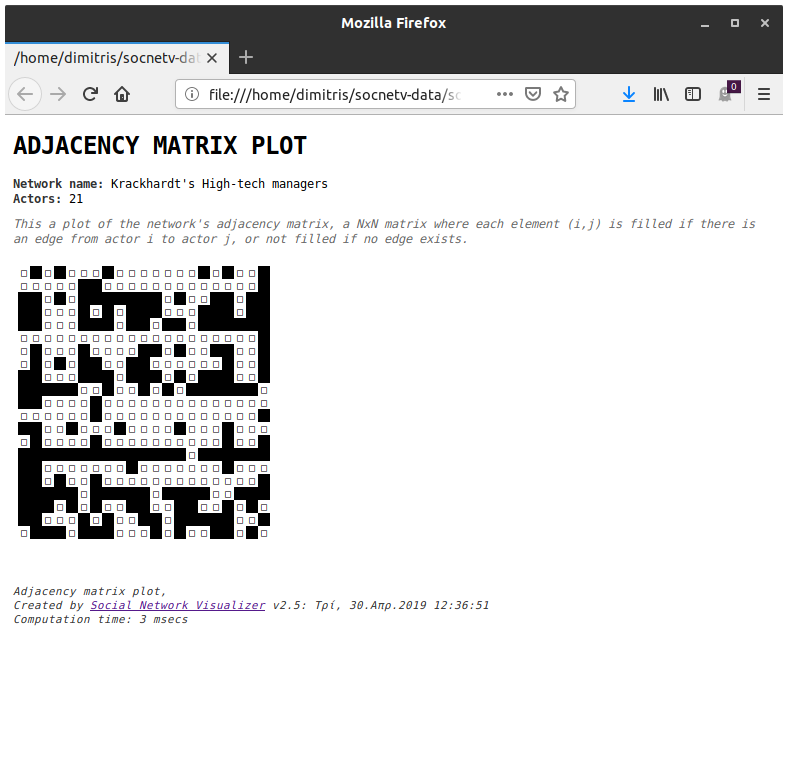
Plot Adjacency

To plot the adjacency matrix, you can also press Shift+F6. The plot will appear in your web browser.

---

Transpose Adjacency

This option computes the transpose of the adjacency matrix.

---

Cocitation Matrix

Computes the Cocitation matrix, $C = A^T \cdot A$.

The matrix $C$ is an $n \times n$ symmetric matrix where each element $c(i,j)$ is the number of actors that have outbound ties/links to both actors $i$ and $j$. The diagonal elements $c_{ii}$ of the Cocitation matrix are equal to the number of inbound edges of $i$ (inDegree).

---

Degree Matrix

This option computes the Degree matrix of the network. The Degree Matrix is a diagonal matrix that contains information about the degree of each graph vertex (row of the adjacency matrix).

---

Laplacian Matrix

This option computes the Laplacian matrix of the network. The Laplacian is an $N \times N$ matrix $L = D - A$, where $D$ is the degree matrix of $A$.

---

Cohesion Measures

The next option in the Analyze menu focuses on basic network/graph measures, such as the geodesic distance between nodes, the mean distance between all nodes, the diameter of the graph, the number of geodesics between nodes, and the eccentricity of each node. Each option is explained below.

---

Reciprocity

Reciprocity, $r$, is a measure of the likelihood of vertices in a directed network to be mutually linked.

SocNetV supports two different methods to index the degree of reciprocity in a social network:

• Arc reciprocity: The fraction of reciprocated ties over all actual ties in the network.

• Dyad reciprocity: The fraction of actor pairs that have reciprocated ties over all pairs of actors that have any connection.

In a directed network, the arc reciprocity measures the proportion of directed edges that are bidirectional. If the reciprocity is 1, then the adjacency matrix is structurally symmetric.

Likewise, in a directed network, the dyad reciprocity measures the proportion of connected actor dyads that have bidirectional ties between them.

In an undirected graph, all edges are reciprocal. Thus the reciprocity of the graph is always 1.

Reciprocity can be computed on undirected, directed, and weighted graphs.

---

Symmetry Test

The Symmetry Test reports whether the network is symmetric or not. A network is called “symmetric” if for every edge $(i,j)$ in the set $E$ of the corresponding graph $G(V,E)$, the opposite $(j,i)$ edge also exists in $E$. In other words, when the adjacency matrix is symmetric.

---

Distance

Computes the geodesic distance (length of the shortest path) between two actors.

In graph theory, the shortest path between two vertices of the graph is called a geodesic.

Thus, the geodesic distance of two nodes in a social network is the length of the shortest path between the corresponding vertices in the graph $G(V,E)$.

By clicking on the Analyze -> Cohesion -> Distance option (or pressing Ctrl+G, Ctrl+G), you will be asked for source and target nodes. Then their distance will be calculated and displayed.

---

Average Distance

The average or mean distance in a social network is the average length of all shortest paths (geodesics) between all pairs of connected vertices in the corresponding graph.

In undirected or strongly connected directed networks, the formula used to compute Average Graph Distance is:

$$\bar{d} = \frac{\sum_{u \neq v}{d(u,v)}}{n \cdot (n-1)}$$

where the denominator is the sum of all pairs of vertices.

It can be proved that in connected networks of $n$ actors, the least upper bound of the Average Distance is $\frac{n+1}{3}$ (Doyle & Graver, 1977).

In the case of disconnected networks/graphs, the denominator used is the total number of existing paths between connected vertices.

In graph theory, the Average Distance is considered to be a natural measure of the compactness of a graph.

---

Distances Matrix

The Analyze -> Cohesion -> Distances Matrix menu option displays the matrix of geodesic distances between all pairs of nodes in the social network.

A distances matrix is an $N \times N$ square matrix, in which the $(i,j)$ element is the distance from node $i$ to node $j$.

---

Geodesics Matrix

This option displays an $n \times n$ square matrix, where the $(i,j)$ element is the number of geodesics between node $i$ and node $j$. The produced matrix, called the sigma matrix, is used in Centralities calculation (see below).

---

Eccentricity

The eccentricity or association number of each node $u$ is the largest geodesic distance between that node and every other node in the network.

$$\epsilon_u = \max{\{d(u,v), \forall v \in V\}}$$

Therefore, the measure reflects how far, at most, each node is from every other node.

The Eccentricity can be calculated in both graphs and digraphs but is usually best suited for undirected graphs.

It can also be calculated in weighted graphs, although the weight of each edge $(v,u)$ in $E$ is always considered to be 1.

---

Diameter

The diameter of a social network is the maximum eccentricity of any vertex in the corresponding graph $G(V,E)$, that is, the maximum distance between any two connected nodes.

$$D = \max{\{d(u,v), \forall u,v \in V\}}$$

---

Connectedness

Checks whether the network is a connected graph, a weakly connected digraph, or a disconnected graph/digraph.

In graph theory, a graph is connected if there is a path between every pair of nodes.

A digraph is strongly connected if there is a path from $i$ to $j$ and from $j$ to $i$ for all pairs of nodes $(i,j)$.

A digraph is weakly connected if at least a pair of nodes are joined by a semipath.

A digraph or a graph is disconnected if at least one node is isolated.

---

Walks of a Given Length

Clicking this option asks for a desired walk length (max: $n-1$). Then SocNetV calculates and displays a square matrix where each element $(i,j)$ is the number of walks of the given length between the corresponding pair of nodes $i$ and $j$.

A walk is a sequence of alternating vertices and edges such as:

$$v_0e_1, v_1e_2, v_2e_3, \dots, e_kv_k$$

where each edge, $e_i$, is defined as $e_i = \{v_{i-1}, v_i\}$.

This function calculates the number of walks of the given length between each pair of nodes, by studying the powers of the sociomatrix.

---

Total Walks

Calculates and displays an $n \times n$ square matrix whose elements denote the number of walks of any length between each pair of nodes. The algorithm is based on the powers of the sociomatrix.

Warning: This function is VERY SLOW on large networks ($n > 50$), since it will calculate all powers of the sociomatrix up to $n-1$ in order to find out all possible walks. If you need to make a simple reachability test, we advise you to use the Reachability Matrix function instead.

---

Reachability Matrix

Calculates the reachability matrix $X^R$ of the graph where each $(i,j)$ element is 1 if nodes $i$ and $j$ are reachable, otherwise 0.

This function is based on the Distances Matrix; it checks whether the corresponding element of the Distances matrix is not zero. If it is not zero, then the nodes $(i,j)$ are reachable, and the $X^R$ element is 1.

---

Clustering Coefficient

In graph theory, a clustering coefficient reflects the degree to which the nodes tend to cluster together. In social network analysis, it is often used to characterize the transitivity of a network.

There are two versions of the Clustering Coefficient: the global and the local.

The global Clustering Coefficient (often called transitivity, see Wasserman and Faust, 1994, page 243) is based on triplets of nodes to give an indication of the overall clustering in the whole network.

A triplet consists of three connected nodes. A triangle, therefore, includes three closed triplets, one centered on each of the nodes.

The global clustering coefficient is the number of closed triplets (or 3 x triangles) over the total number of triplets (both open and closed). This metric can be applied to both undirected and directed networks.

The local Clustering Coefficient (introduced by Duncan J. Watts and Steven Strogatz in 1998) is an indication of the embeddedness of single nodes, and it is also used as an indication of the network transitivity.

Specifically, the Clustering Coefficient $C$ of a node quantifies how close the node and its neighbors are to being a complete subgraph (clique).

Let $k_i$ be the number of vertices, $|N_i|$, in the neighborhood, $N_i$, of a node $i$.

In a directed network, the clustering coefficient is computed with the formula:

$$C_i = \frac{|\{e_{jk}: v_j,v_k \in N_i, e_{jk} \in E\}|}{k_i(k_i-1)}$$

In undirected networks, the formula is:

$$C_i = \frac{2|\{e_{jk}: v_j,v_k \in N_i, e_{jk} \in E\}|}{k_i(k_i-1)}$$

If the network relation represents friendships among actors, the clustering coefficient $C_i$ of an actor $i$ measures the ratio of existing friendships between any two of that actor’s friends relative to all possible friendships between her friends (the situation where the subgraph is complete).

A value close to one indicates that the node is involved in many transitive relations.

SocNetV also computes the network average clustering coefficient (Watts and Strogatz):

$$\bar{C} = \frac{1}{n} \sum_{i=1}^{n} C_i$$

Note: The clustering can be used to determine whether a network is a small-world or not.

For the ring lattice, the clustering coefficient is:

$$C(0) = \frac{3(K-2)}{4(K-1)}$$

tending to $\frac{3}{4}$ as $K$ grows, where $K$ is the mean degree.

---

All the basic network statistics, such as nodes, edges and density are displayed and automatically updated in the Analysis tab of the left dock in SocNetV main window.

---

Centralities and Prestige

The last option in the Analysis menu opens the “Centrality and Prestige” sub-menu.

In social network analysis (SNA), researchers use various measures to assess the prominence or importance of each node (actor) within a network. These measures help identify influential individuals or key entities in the network. For example, in a social network, we might want measure the importance of a person based on the number of friends they have, or we could want to identify a person who is highly respected by others in the network. In another example, we might want to know how critical a power station is inside the power company grid…

Although there are various metrics for calculating node importance, they are generally classified into two broad categories: Centrality and Prestige. These concepts are foundational in social network analysis, drawing on the work of Wasserman and Faust (1994), as well as Knoke and Burt (2001), who distinguish between centrality as a measure of connectivity and prestige as a measure of status or recognition within a network.

Centrality

Centrality measures quantify the relative importance of a node based on its position within the network. Central nodes are typically well-connected, either through direct connections or by bridging gaps between other nodes.

SocNetV supports a wide variety of centrality indices, including those conceptualized by Wasserman and Faust, such as:

• Degree Centrality (DC): Measures the number of direct connections a node has. A node with high degree centrality is considered well-connected within the network.

• Closeness Centrality (CC): Measures how close a node is to all other nodes, based on the length of the shortest paths. A node with high closeness centrality can reach other nodes quickly.

• Betweenness Centrality (BC): Measures how often a node lies on the shortest path between two other nodes. Nodes with high betweenness centrality have significant control over information flow within the network.

• Eigenvector Centrality (EVC): Measures the influence of a node by considering both the number of connections it has and the importance of the nodes it is connected to. A node connected to other high-scoring nodes will have a higher score.

• Eccentricity Centrality (EC): Measures the longest shortest path from a node to all other nodes in the network. The node with the lowest eccentricity is considered the most “central” in terms of distance.

• Proximity Prestige (PP): Measures how close a node is to other influential nodes within its influence domain. A node with high proximity prestige is close to important nodes in the network.

• Influence Range Closeness Centrality (IRCC): A variation of Closeness Centrality that considers only the nodes reachable from a given node, making it useful for disconnected networks.

• Stress Centrality (SC): Measures how often a node appears on the shortest paths between other nodes. High stress centrality indicates a node is a key intermediary or bridge within the network.

These centrality measures focus on the node’s direct connections, its geodesic distances, or its ability to influence others through its position in the network. Wasserman and Faust’s conceptualization of centrality focuses on connectivity and control, with a particular emphasis on how nodes serve as intermediaries or closers in the network.

Prestige

In contrast, Prestige measures focus on the recognition or status of a node, often derived from the nodes that point to it ( “choices received” or nominations to it), rather than the ones it points to (“choices made” by it). Prestige is particularly useful in directed networks, where relationships between nodes have direction (e.g., citations or recommendations).

As Wasserman and Faust (1994) argue, prestige measures reflect the notion of “visibility” or “respect,” as seen in networks of social influence or reputation. SocNetV supports several prestige measures, including:

• Degree Prestige (DP): Also known as InDegree Centrality, this measure counts the number of inbound connections (or nominations) to a node. Nodes with higher in-degree are considered more prestigious.

• PageRank Prestige (PRP): Measures the importance of a node based on the quantity and quality of its inbound links, normalized by the number of outgoing links from the referring nodes.

• Proximity Prestige (PP): Measures how close a node is to other influential nodes, reflecting its reachability and position within the influence domain.

Comparison of Centrality vs. Prestige Measures

The table below compares the key characteristics of centrality and prestige measures:

Feature	Centrality	Prestige
Focus	Quantifies how well-connected a node is within the network	Quantifies the status or importance based on the node’s inbound connections
Type of Networks	Typically used in undirected or directed networks	Primarily used in directed networks (but also weighted graphs)
Common Measures	Degree Centrality (DC), Closeness Centrality (CC), Betweenness Centrality (BC), Eigenvector Centrality (EVC), Eccentricity Centrality (EC), Proximity Prestige (PP), Influence Range Closeness Centrality (IRCC)	Degree Prestige (DP), PageRank Prestige (PRP), Proximity Prestige (PP)
Application	Identifies nodes that are influential in terms of connectivity	Identifies nodes that are influential based on being highly valued or referenced by others
Mathematical Basis	Based on direct connections or shortest paths between nodes	Based on the flow of influence or status across the network
Example in Social Networks	A node with many friends (DC), a person who is close to everyone (CC), or a broker (BC)	A highly referenced academic paper (PRP), a person who receives many nominations (DP)
Strengths	Identifies direct connections and key intermediaries	Measures a node’s reputation or recognition in the network
Limitations	Can overlook the quality of connections or directed influence	Primarily applies to directed or weighted networks, not undirected ones

---

This distinction between centrality and prestige measures, following the work of Wasserman and Faust (1994), illustrates the different ways in which nodes can be important within a network. Centrality focuses on how well a node is connected or positioned, while prestige emphasizes how much recognition a node receives from others.

For digraphs, where the relations are directional, most centrality measures are calculated by focusing on “choices made” (or outEdges).

Given that Prestige measures are based on the inbound ties to each node from all others, these indices are meaningfull on directed graphs.

Note

Centrality measures are calculated for each node (node Centrality) and for the whole network (group Centrality). Thus, when you click on a centrality option, SocNetV will calculate the corresponding index of every node and the whole network, and it will display the report in a new browser window (using the system’s default web browser). By default, analysis files are saved in the socnetv-data/ subfolder.

Degree Centrality (DC)

The DC measure quantifies how many ties a node has to other nodes in the network. In social network theory, this index is often considered a measure of actor activity. It can be computed in both undirected and directed networks/relations, but is usually best suited for undirected ones.

Mathematically, in undirected graphs, the DC index of each vertex $u$ is the number of edges attached to it.

In directed graphs, the DC is the total number of arcs (outEdges) starting from $u$ (outDegree).

The index can be computed in weighted graphs as well. In that case, the DC of each node $u$ is the sum of weights of all edges/outEdges attached to $u$.

Along with other metrics that are based on the notion of distance (closeness, eccentricity, etc.), the DC falls in the category of reachability measures.

To compute Degree Centralization (or Group Degree Centrality), SocNetV uses Freeman’s formula for unvalued graphs:

$$GDC = \frac{\sum{(\text{maxDC'} - \text{DC'})}}{(N-1) \cdot (N-2) / (2 \cdot N - 1)}$$

Note: In valued (or weighted) graphs, GDC cannot be computed with Freeman’s formula. As a measure of degree centralization, one can use DC variance or mean instead.

Closeness Centrality (CC)

This CC index focuses on how close each node is to all other nodes in the network.

Nodes with high Closeness Centrality are those who can reach many other nodes in few steps. The idea is that a node is more central if it can quickly interact with more of the others. CC is also interpreted as the ability to access information through the “grapevine” of network members.

For each node $u$, the CC score is the inverse sum of geodesic distances from that node to every other node:

$$CC_u = \frac{1}{\sum_{v \in E} {d(u,v)}}$$

This index can be calculated in graphs and strongly connected digraphs (that is, if there is a directed path from $v$ to $u$ for all nodes $v$ and $u$ in the graph). If there are isolated nodes in the network, they are dropped by default. In non-strongly connected digraphs, the ordinary CC is undefined. In that case, you can use the Influence Range Closeness Centrality index.

CC can also be calculated in weighted graphs, although the value of each edge $(u,v)$ is always considered to be 1.

The maximum value of CC is $\frac{1}{N-1}$, when the node is adjacent to all others. Thus, the standardized CC index $CC'$ is calculated by:

$$CC' = (N-1) \times CC$$

Group CC is calculated using Freeman’s general formula in undirected graphs:

$$GCC = \frac{\sum{(\text{maxCC'} - \text{CC'})}}{(N-1) \cdot (N-2) / (2 \cdot N - 1)}$$

Note: As with all centrality measures in directed graphs, CC considers only outbound edges. If you want to analyze inbound edges, use a Prestige measure, i.e., Proximity Prestige.

---

Influence Range Closeness Centrality (IRCC)

For each node $u$, IRCC is the standardized inverse average distance between $u$ and every other node reachable from it.

This improved CC index is optimized for graphs and directed graphs which are not strongly connected. Unlike the ordinary CC, which is the inverted sum of distances from node $v$ to all others (thus undefined if a node is isolated or the digraph is not strongly connected), the IRCC considers only distances from node $u$ to nodes in its influence range $J$ (nodes reachable from $u$).

The IRCC formula used is the ratio of the fraction of nodes reachable by $u$ $\left(\frac{|J|}{n-1}\right)$ to the average distance of these nodes from $u$:

$$\frac{\frac{|J|}{n-1}}{\frac{\sum{d(u,j)}}{|J|}}$$

Betweenness Centrality (BC)

For each node $u$, BC is the ratio of all geodesics between pairs of nodes which run through $u$. It reflects how often that node lies on the geodesics between the other nodes of the network.

The BC score of each actor can be interpreted as a measure of potential control as it quantifies just how much that actor acts as an intermediary to others. An actor which lies between many others is assumed to have a higher likelihood of being able to control information flow in the network.

In essence, BC assumes that communication in a network occurs along the shortest possible path, the geodesic. It totally neglects the possibility of communication along non-geodesic paths between actors. If you need a centrality index that considers all possible paths, use the Information Centrality (IC).

Note that betweenness centrality assumes that all geodesics have equal weight or are equally likely to be chosen for the flow of information between any two nodes. This is reasonable only on “regular” networks where all nodes have similar degrees. On networks with significant degree variance, you might want to try using IC instead.

Also, BC is very sensitive to network dynamics, i.e., it changes a lot when we add or remove a vertex or an edge.

This index can be calculated in both graphs and digraphs but is usually best suited for undirected graphs. It can also be calculated in weighted graphs, although the weight of each edge $(u,v)$ in $E$ is always considered to be 1.

Formula for Betweenness Centrality:

The BC of a node $u$ is given by the formula:

$$BC_u = \sum_{s \neq u \neq t} \frac{\sigma_{st}(u)}{\sigma_{st}}$$

Where:

• $\sigma_{st}$ is the total number of geodesics between nodes $s$ and $t$.

• $\sigma_{st}(u)$ is the number of geodesics between $s$ and $t$ that pass through node $u$.

---

Stress Centrality (SC)

The SC of each node $u$ is the total number of geodesics between all other nodes which run through $u$. When one node falls on all geodesics between all the remaining $(N-1)$ nodes, then we have a star graph with maximum Stress Centrality. This index reflects how often a node lies on the geodesics between other nodes.

This index can be calculated in both graphs and digraphs but is usually best suited for undirected graphs. It can also be calculated in weighted graphs, although the weight of each edge $(v,u)$ in $E$ is always considered to be 1.

This index was introduced by Shimbel (1953).

Formula for Stress Centrality:

The SC of node $u$ is given by the formula:

$$SC_u = \sum_{s \neq u \neq t} \sigma_{st}(u)$$

Where:

• $\sigma_{st}(u)$ is the number of geodesics between nodes $s$ and $t$ that pass through node $u$.

Note

The formula for SC is very similar to BC in that it counts how many geodesics pass through node uu, but it sums this count over all pairs of nodes in the network.

Eccentricity Centrality (EC) or Harary Graph Centrality

For each node $u$, the Eccentricity Centrality (EC) is the inverse of the largest geodesic distance $(u,v)$ to every other node $v$ in the network. Therefore, the EC score reflects how close each node is to every other node and, hence, to the middle of the network.

Nodes with high EC scores have short distances to other nodes in the graph and are likely to be near the middle of the network. Nodes with low EC scores have longer distances to some other nodes in the graph, and therefore are most likely towards the “edge” of the network.

This index can be calculated in both graphs and digraphs, but it is usually best suited for undirected graphs. It can also be calculated in weighted graphs, although the weight of each edge $(v,u)$ in $E$ is always considered to be 1.

The EC is also known as Graph Centrality (Hage and Harary, 1995).

Formula for Eccentricity Centrality (EC):

The EC of node $u$ is given by the formula:

$$EC_u = \frac{1}{\max_{v \in V} d(u,v)}$$

Where:

• $d(u,v)$ is the geodesic distance between nodes $u$ and $v$.

• $\max_{v \in V} d(u,v)$ is the largest geodesic distance from node $u$ to any other node in the network.

The formula for EC calculates the inverse of the maximum geodesic distance from a node to any other node in the network. This is a measure of how “central” the node is within the graph, with nodes having short distances to all others being more central.

---

Power Centrality (PC)

The Power Centrality (PC) is a generalized degree centrality measure suggested by Gil and Schmidt.

For each node $u$, this index sums its degree (with weight 1), with the size of the 2nd-order neighborhood (with weight 2), and in general, with the size of the $k$-th order neighborhood (with weight $k$).

Thus, for each node $u$, the most important other nodes are its immediate neighbors and then, in decreasing importance, the nodes of the 2nd-order neighborhood, 3rd-order neighborhood, etc. For each node, the sum obtained is normalized by the total number of nodes in the same component minus 1.

This index can be calculated in both graphs and digraphs but is usually best suited for undirected graphs. It can also be calculated in weighted graphs, although the weight of each edge $(u,v)$ in $E$ is always considered to be 1 (therefore not considered).

Formula for Power Centrality (PC):

The PC of node $u$ is given by:

$$PC_u = \sum_{k=1}^{\infty} k \cdot |N_k(u)|$$

Where:

• $N_k(u)$ is the set of nodes that are at a distance $k$ from node $u$.

• The sum is taken over all neighborhood sizes from $k = 1$ to the maximum neighborhood size.

This approach emphasizes nodes that are connected to important neighbors, with each successive neighborhood contributing less to the centrality score.

Information Centrality (IC)

The Information Centrality (IC) is an index suggested by Stephenson and Zelen (1989) which focuses on how information might flow through many different paths. Unlike SC and BC, the IC metric uses all paths between actors, weighted by strength of tie and distance.

The IC’ score is the standardized IC (IC divided by the sum of all IC scores) and can be seen as the proportion of total information flow that is controlled by each actor.

Note that standard IC’ values sum to unity, unlike most other centrality measures.

Since there is no known generalization of Stephenson & Zelen’s theory for information centrality to directional relations, the index should be calculated only for undirected graphs and is more meaningful in weighted graphs/networks.

Note: To compute this index, SocNetV drops all isolated nodes and symmetrizes (if needed) the adjacency matrix even when the graph is directed (Wasserman & Faust, p. 196).

Algorithm: In order to calculate the IC index of each actor, we create an $N \times N$ matrix $A$ from the (symmetrized) sociomatrix with:

$$A_{ii} = 1 + d_i$$ $$A_{ij} = \begin{cases} 1 & \text{if } (i,j) = 0 \\ 1 - w_{ij} & \text{if } (i,j) = w_{ij} \end{cases}$$

Next, we compute the inverse matrix of $A$, for instance $C$, using LU decomposition. Note that we can always compute $C$ since the matrix $A$ is always a diagonally strong matrix, hence it is always invertible.

Finally, IC is computed by the formula:

$$IC_i = \frac{IC_i - 1}{C_{ii} + \frac{T - 2 \cdot R}{N}}$$

Where:

• $T$ is the trace of matrix $C$ (the sum of diagonal elements).

• $R$ is the sum of the elements of any row (since all rows of $C$ have the same sum).

IC has a minimum value but not a maximum.

---

Eigenvector Centrality or Gould index (EVC)

The Eigenvector Centrality (EVC) of each node is defined as the $i$-th element of the leading eigenvector of the adjacency matrix. The leading eigenvector is the eigenvector corresponding to the largest positive eigenvalue.

The Eigenvector Centrality, proposed by Bonacich (1989), is an extension of the simpler Degree Centrality because it gives each actor a score proportional to the scores of its neighbors.

Thus, a node may be important, in terms of its EVC, because it has lots of ties or it has fewer ties to important other nodes.

Formula for Eigenvector Centrality (EVC):

The EVC of node $u$ is calculated as the $i$-th element of the eigenvector corresponding to the largest eigenvalue of the adjacency matrix $A$, i.e., we solve the following eigenvalue equation:

$$A \mathbf{v} = \lambda \mathbf{v}$$

Where:

• $A$ is the adjacency matrix.

• $\mathbf{v}$ is the eigenvector corresponding to the largest eigenvalue $\lambda$.

• The EVC of node $u$ is the value of the $u$-th element of the eigenvector $\mathbf{v}$.

Thus

$$x_i = \frac{1}{\lambda} \sum_{j \in N(i)} x_j$$

Where:

• $x_i$ is the centrality score of node $i$,

• $N(i)$ is the set of neighbors of node $i$,

• $\lambda$ is the largest eigenvalue of the adjacency matrix $A$.

---

Degree Prestige (DP) or InDegree Centrality

For each node $u$, this metric counts the number of inbound arcs at $u$. The index is meaningful in directed graphs as a measure of the prestige of each node. Thus, it is called Degree Prestige (also known as InDegree Centrality).

Note that in undirected graphs, the DP index is identical to Degree Centrality.

Actors with higher DP are considered more prominent among others because they receive more nominations or choices (i.e., they have a larger inDegree). The larger the index, the more prestigious the node/actor.

This index can be calculated only for unvalued or valued digraphs. In weighted relations, DP is the sum of weights of all arcs/inLinks ending at node $v$.

Note: In unvalued graphs, SocNetV computes Group Degree Prestige using Freeman’s formula.

Note: For valued or weighted graphs, we cannot calculate Group Degree Centrality (DC) using Freeman’s formula. You can use DP variance or mean instead.

---

PageRank Prestige (PRP)

The PageRank Prestige (PRP) is an importance ranking for each node based on the structure of its incoming links/edges and the rank of the nodes linking to it.

The original PageRank algorithm, developed by Page and Brin (1997), focuses on how nodes are connected to each other, treating each link from a node as a citation/backlink/vote to another.

In essence, for each node, the algorithm counts all incoming links (edges) to it, but it does so by not counting all links equally. It normalizes each in-link from a node by the total number of its outgoing edges.

The PR index for each node $u$ is computed iteratively by the formula:

$$PR_u = \frac{1 - d}{N} + d \cdot \sum_{v \in M_u} \frac{PR_v}{DC_v}$$

Where:

• $u$ is the node,

• $d$ is the damping factor ($d = 0.85$),

• $N$ is the number of vertices in the network,

• $M_u$ is the set of all nodes which link to $u$,

• $DC_v$ is the out-degree of node $v$.

The PR values correspond to the principal eigenvector of the normalized link matrix.

This index can be calculated in both graphs and digraphs but is usually best suited for directed graphs since it is a prestige measure.

The PageRank Prestige index can also be calculated in weighted graphs.

Note: In weighted relations, each backlink to node $u$ from node $v$ is considered to have weight = 1, but it is normalized by the sum of out-degree weights (outEdges) of node $v$. Therefore, nodes with high out-link weights give a smaller percentage of their PR to node $u$.

---

Proximity Prestige (PP)

The Proximity Prestige (PP) index measures how proximate a node $u$ is to the nodes in its influence domain $I$ — the influence domain of a node is the number of other nodes that can reach it. In this metric, the proximity of each node $u$ is based on distances to, rather than from, it. To put it simply, in PP, what matters is how close all the other nodes are to node $u$.

The algorithm takes the average distance to node $u$ of all nodes in its influence domain, standardizes it by multiplying with $\frac{(N-1)}{|I|}$, and takes its reciprocal.

In essence, the formula SocNetV uses to calculate PP for every node $u$ is the ratio of the fraction of nodes that can reach node $u$ to the average distance of those nodes to $u$:

$$PP = \frac{\frac{|I|}{N-1}}{\frac{\sum{d(v,u)}}{|I|}}$$

Where the sum is over every node $v$ in $I$.

---

Community Detection

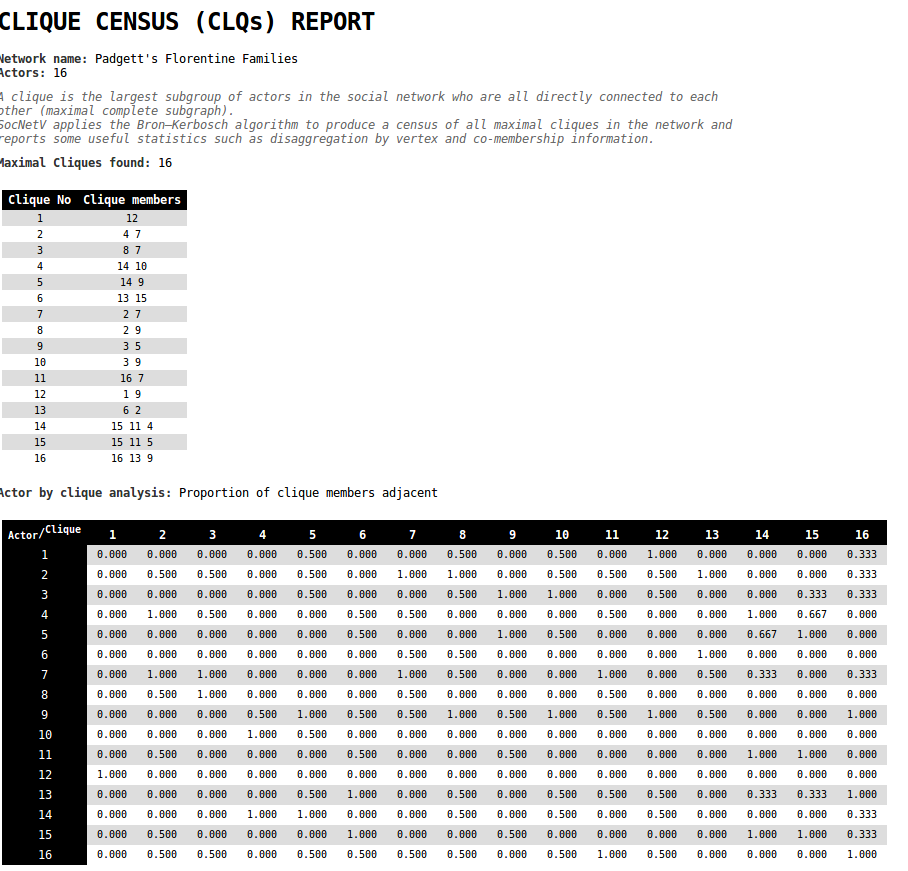
Clique Census

A clique is a group of people who interact with each other more regularly and intensely than with other people not belonging to the clique. In mathematical terms, a clique is a subset of vertices in an undirected graph $G$, where every two distinct vertices in the clique are adjacent to each other, forming a complete subgraph.

In Social Network Analysis, a clique refers to the largest subgroup of actors who are all directly connected to each other. A maximal clique is a clique that cannot be extended by including one more actor. Maximal cliques overlap and form closed triads, and the term maximal means that no additional actors can be added without breaking the clique’s completeness.

SocNetV uses the Bron–Kerbosch algorithm to find all maximal cliques in both undirected and directed graphs. The algorithm computes a census of maximal cliques, producing useful statistics and co-membership information about the cliques.

Caution

The computation of maximal cliques can be slow in very large or dense social networks due to the NP-complete nature of the clique problem.

---

Triad Census

A triad is a set of three nodes in a network. Triads are essential for understanding the local structure of a network, as they capture the relationships between three actors. In a network of $N$ actors, there are $C(N, 3) = 60$ possible triads, where $C(N, 3)$ represents the combination formula for selecting 3 nodes from $N$ actors:

$$C(N, 3) = \frac{N!}{3!(N-3)!}$$

The Triad Census is used to identify and count all possible types of triads in a network.

There are 16 different triad types (isomorphism classes), each labeled according to the M-A-N labeling scheme, as described by Holland, Leinhardt, and Davis, which categorizes the triads as follows:

• M: Number of mutual (M) dyads in the triad (possible values: 0, 1, 2, 3)
• A: Number of asymmetric (A) dyads in the triad (possible values: 0, 1, 2, 3)
• N: Number of null (N) dyads in the triad (possible values: 0, 1, 2, 3)
• Fourth character: Infers features such as cycle or transitivity (possible values: none, D (Down), U (Up), C (Cyclic), T (Transitive))

The following list shows all the 16 triad types:

Within each row, all the triad types have the same number of arcs present:

003
012
102     021D  021U  021C
111D    111U  030T  030C
201     120D  120U  120C
210
300

So, when you click on the Triad Census menu option, SocNetV calculates and displays a vector $T$ of length 16. Each element $T_u$ is the frequency of a specific triad type in the network, e.g., $T_{003} = 3$.

Furthermore, the order of the elements of vector T is the same as the aforementioned ordering of the triad types:

T = [ T003, T012, T102, T021D, T021U, T021C, T111D, T111U, T030T, T030C, T201, T120D, T120U, T120C, T210, T300 ]

The sum of all these frequencies equals $C(N,3)$, the total number of possible triads in the network.

---

Structural Equivalence Methods

A key notion in Social Network Analysis (SNA) is that of structural equivalence. The idea is to map the relationships in a graph by creating classes or groups of actors who are equivalent in some sense.

One way to identify these groups is by examining the relationships between actors for similarity patterns.

There are many methods to measure the similarity or dissimilarity of actors in a network.

SocNetV supports the following methods:

• Similarity by measure

• Pearson Correlation Coefficients

• Tie profile dissimilarities

By applying one of these methods, SocNetV creates a pairwise actor similarity/dissimilarity matrix.

Actor Similarity (by Measure)

This method computes a pairwise actor similarity matrix, where each element $(i, j)$ is the ratio of tie (or distance) matches of actors $i$ and $j$ to all other actors.

SocNetV supports the following measures:

• Simple Matching (Exact Matches): Proportion of tie/distance matches (present or absent) between two actors.

• Jaccard Index (Positive Matches or Co-citation): Percentage of same ties/distances reported by both actors to the total number of ties reported.

• Hamming Distance: Number of ties/distances that differ between each pair of actors.

• Cosine Similarity

• Euclidean Distance

For example, in the case of Simple Matching, the similarity matrix depicts the ratios of exact matches of pairs of actors to all other actors. If the element $(i, j) = 0.5$, it means that actors $i$ and $j$ have the same ties present or absent 50% of the time.

These measures of similarity are particularly useful when ties are binary (not valued).

Note

In very sparse networks (with low density), measures such as exact matches, correlation, and distance will show little variation among the actors, making it difficult to classify the actors into structural equivalence classes.

Pearson Correlation Coefficients

This method computes a correlation matrix, where the elements are the Pearson correlation coefficients between pairs of actors in terms of their tie profiles or distances (in, out, or both).

The Pearson product-moment correlation coefficient (PPMCC or PCC, or simply Pearson’s $r$) is a measure of the linear dependence or association between two variables $X$ and $Y$.

This correlation measure of similarity is particularly useful when ties are valued/weighted, denoting strength, cost, or probability.

Tie Profile Dissimilarities

This method computes a matrix of tie profile distances/dissimilarities between all pairs of actors/nodes in the social network using an ordinary metric such as Euclidean distance, Manhattan distance, Jaccard distance, or Hamming distance.

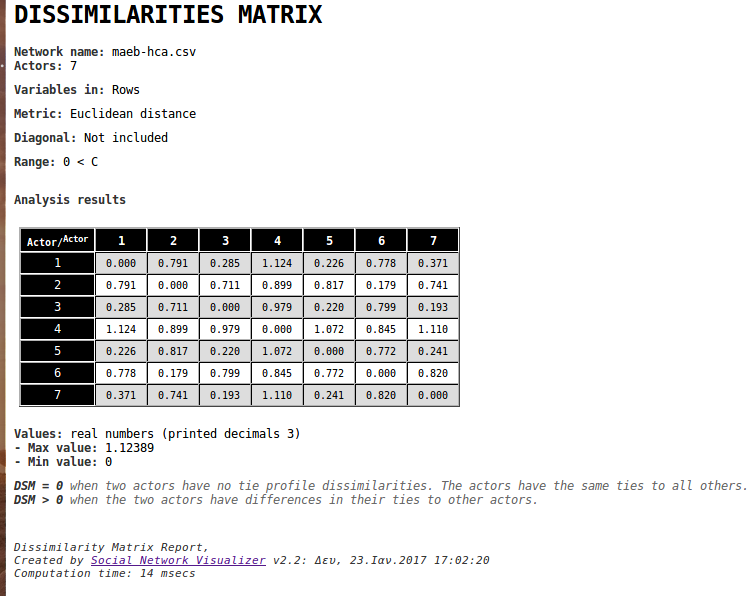
The resulting distance matrix is an $n \times n$ matrix, where the element $(i, j)$ is the distance or dissimilarity between the tie profiles of node $i$ and node $j$.

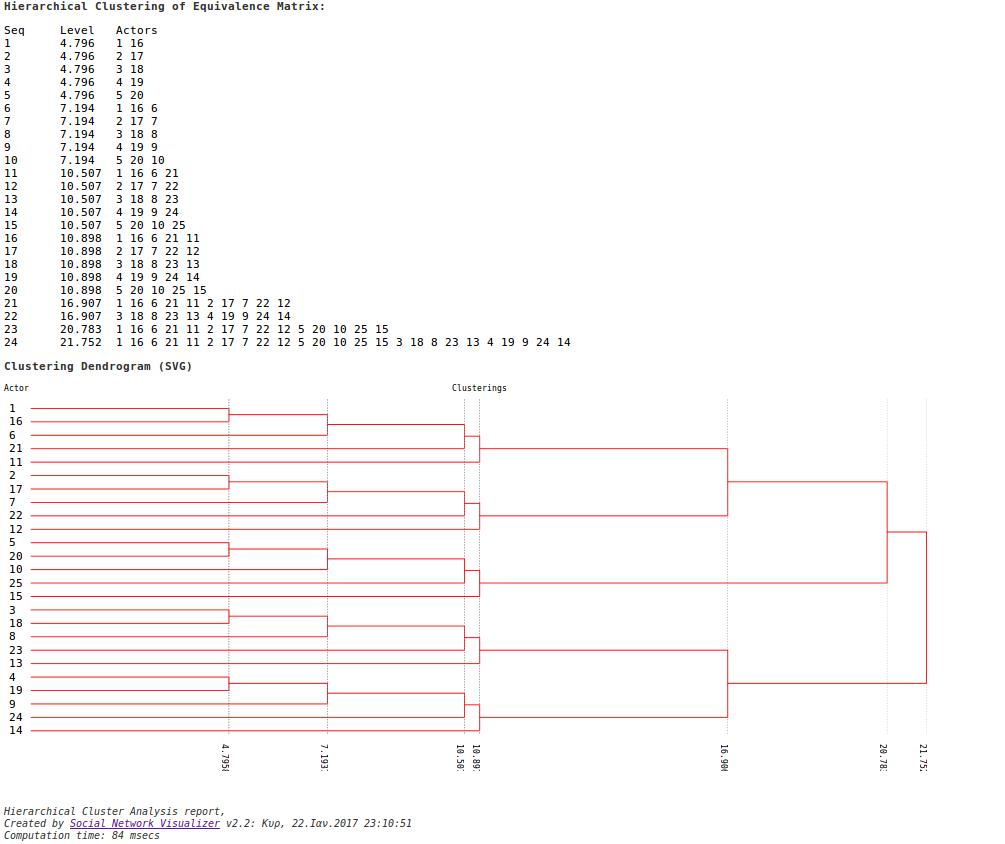
Hierarchical Cluster Analysis (HCA)

Hierarchical Clustering (or Hierarchical Cluster Analysis, HCA) is a method of cluster analysis that builds a hierarchy of clusters based on their elements’ dissimilarity. In the context of SNA, these clusters usually consist of network actors.

This method takes the social network distance matrix as input and uses the Agglomerative “bottom-up” approach, where each actor starts in its own cluster (Level 0). In each subsequent level, as we move up the clustering hierarchy, a pair of clusters are merged into a larger cluster, until all actors end up in the same cluster.

To decide which clusters should be combined at each level, a measure of dissimilarity between sets of observations is required. This measure consists of a metric for the distance between actors (e.g., Manhattan distance) and a linkage criterion (e.g., single-linkage clustering).

This linkage criterion (essentially a definition of distance between clusters) differentiates between the different HCA methods.

The result of Hierarchical Cluster Analysis is the clusters per level and a dendrogram:

Caution

The complexity of agglomerative clustering is $O(n^2 \log n)$, which makes it too slow for large data sets.