Network Generation

The application can recreate famous social network analysis datasets (e.g., Knoke: Bureaucracies Network) or generate random networks using graph theory models such as the Barabási–Albert model for scale-free networks and the Watts-Strogatz model for small-world networks.

SocNetV can also create “networks” of linked webpages using the built-in Web Crawler, which maps hypertext links between webpages starting from a given webpage or website.

Recreating Famous Datasets

SocNetV allows you to recreate a variety of well-known social network datasets. These networks are commonly used in social network analysis (SNA) research and provide valuable insights into real-world relationships and structures. Here’s the list of supported datasets and their background:

Krackhardt: High-tech Managers
A network of 21 managers in a US high-tech company. It captures advice, friendship, and hierarchical “reports-to” relationships. This dataset is frequently used to study organizational behavior and power dynamics within corporate structures.
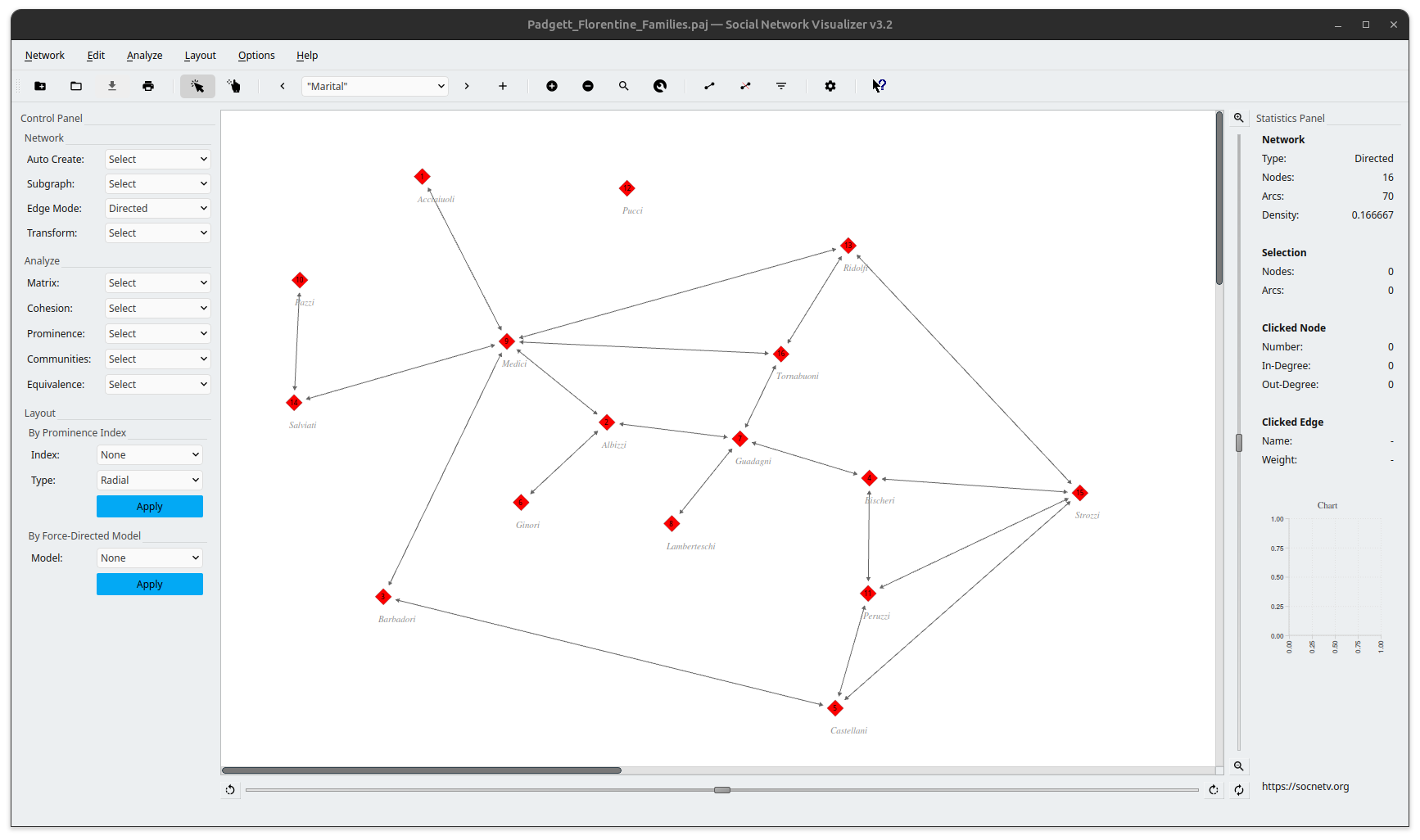
Padgett: Florentine Families
This Renaissance-era dataset maps marital and business ties among 16 influential families in Florence, Italy. It illustrates the interplay of economic and social alliances and highlights the Medici family’s pivotal role in political stability and dominance.
Zachary: Karate Club
A well-known network of 34 members from a university karate club, this dataset famously illustrates a social group’s division into two factions following a conflict. It is a classic example in SNA research for studying community structures and group dynamics.
Bernard: Killworth Fraternity
A multirelational dataset of 58 fraternity members, capturing various social ties such as friendships, advice, and collaborations. It is often used to analyze multiplex relationships in small, close-knit communities.
Galaskiewicz: CEOs and Clubs
This affiliation dataset represents social and professional connections among CEOs and their spouses through memberships in exclusive clubs and corporate boards. It highlights the role of elite networks in power consolidation and influence.
Freeman’s EIES Network
A multirelational network of 32 social scientists collaborating on the “Experimental Interpersonal Environment Study” (EIES). It captures advice, trust, and other professional relationships among participants.
Knoke: Bureaucracies Network
A network depicting information and monetary relationships among 10 US organizations. This dataset is instrumental in studying interorganizational exchange and network governance.
Mexican Power Network
This historical network reveals the power structure in Mexico during the 1940s, including relationships between political figures, business elites, and institutions.
Campnet
Captures interactions among 18 individuals during a 3-week workshop. The dataset records the frequency and duration of time spent together, making it a useful case for studying informal socialization and group cohesion.
Herschel Graph
A mathematical graph representing the smallest non-Hamiltonian polyhedral graph, with 11 nodes and 18 edges. It is a classic example in graph theory and topology studies.
Thurman: Office Networks and Coalitions
This network represents interactions among 15 employees in an international corporation. It captures both formal organizational ties and informal coalitions, offering insights into workplace dynamics.
Additional Datasets
SocNetV includes several other well-known datasets for research and educational purposes, not explicitly listed here.

SocNetV continues to expand its library of predefined datasets to support a variety of network analysis needs. Stay tuned for the coming releases to uncover more networks and experiment with their unique structures and properties.

To recreate a dataset:

From the File menu, select “Create Known Dataset” or press F7.
A dialog will appear where you can select a dataset from the list above.
Press “OK,” and the selected network will be displayed on the canvas.

Random Network Creation

SocNetV can generate random networks based on various graph theory models, including:

Scale-Free (S-F) Networks

A scale-free network has a degree distribution that follows a power law. Actors with degrees much higher than average are common and are known as “hubs.”

The probability $P(k)$ that a node has degree $k$ is:

P(k) \sim k^{-\gamma}

where $\gamma$ typically satisfies $2 < \gamma < 3$ .

SocNetV generates scale-free networks using the Barabási–Albert (BA) model. The algorithm begins with $m_0$ connected nodes. In each step, a new node is added with $m$ edges. The probability $p_i$ that the new node connects to an existing node $i$ is:

p_i = \frac{\alpha + d_i^p}{\sum_j d_j}

where:

$\alpha$ : Initial attractiveness of each node.
$d_i$ : Degree of node $i$ .
$\sum_j d_j$ : Sum of all node degrees.

If $\alpha = 0$ and $p = 1$ , the preferential attachment is linear, which corresponds to the BA model.

Small-World (SW) Networks

Small-world random networks are characterized by short average path lengths and high clustering. SocNetV uses the Watts-Strogatz model to generate such SW random networks.

Given $N$ nodes, mean degree $K$ (assumed to be an even integer), and a rewiring probability $\beta$ , satisfying $0 \le \beta \le 1$ and $N\gg K \gg \ln(N)\gg 1$ , the model generates an undirected graph with $N$ nodes and $\frac{NK}{2}$ edges as follows:

Create a regular ring lattice with $N$ nodes, each connected to $K/2$ neighbors on each side.
For each edge $(n_i, n_j)$ with $i < j$ , rewire it with probability $\beta$ . Rewiring replaces $(n_i, n_j)$ with $(n_i, n_k)$ , where $k$ is chosen uniformly, avoiding self-loops ( $k \neq i$ ) and duplicate edges.

To generate a small-world network, go to Network > Create Random Network > Small World, then specify the number of nodes ( $N$ ), mean degree ( $K$ ), and rewiring probability ( $\beta$ ).

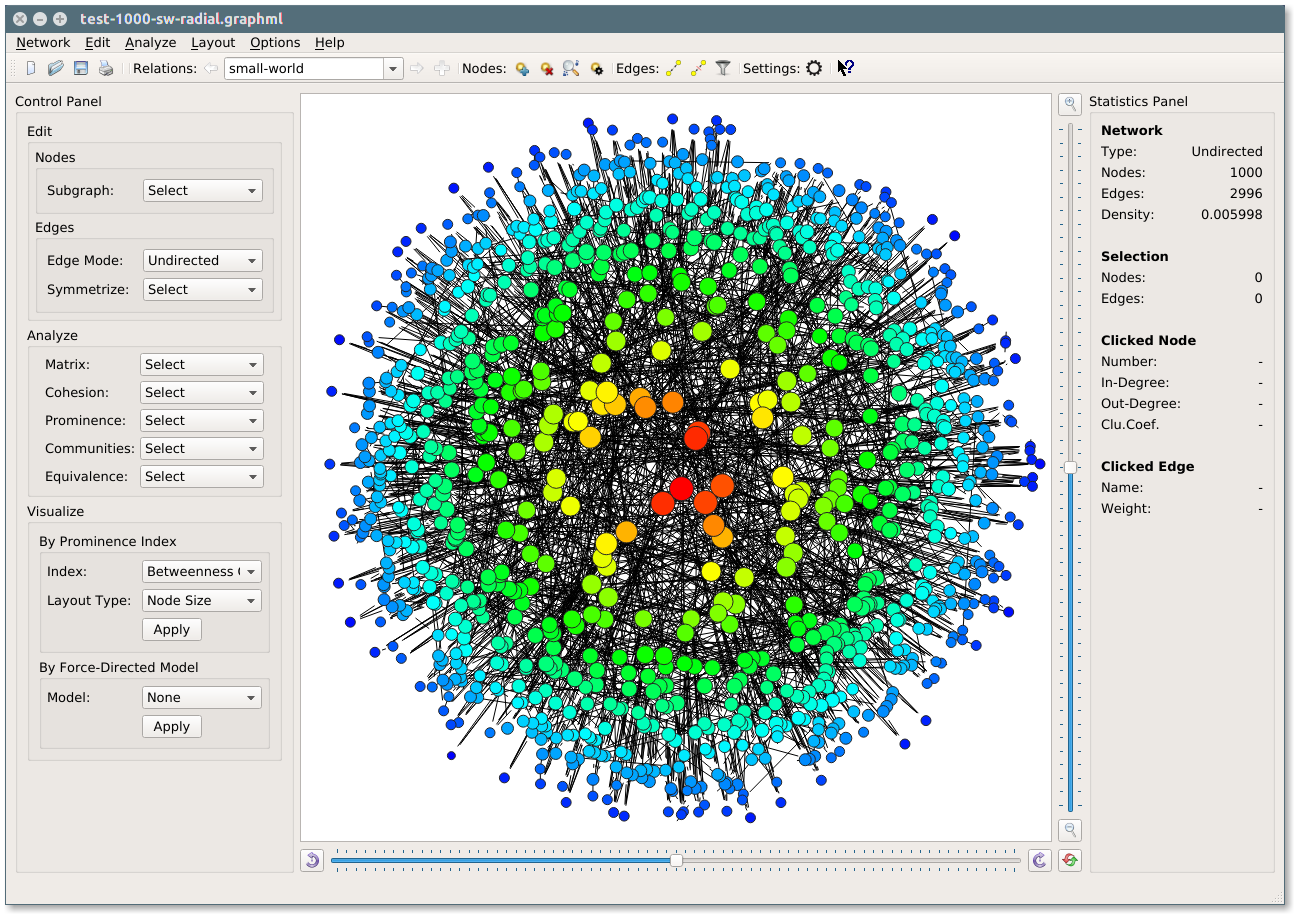Example: Small-world random network of 1000 actors created by SocNetV. Actor positions, colors and sizes reflect their betweenness centrality

Erdős–Rényi (ER) Networks

The Erdős–Rényi model generates random networks based on either of two modes:

$G(n, M)$ : A graph with $n$ nodes and $M$ edges, where all graphs are equally likely.
$G(n, p)$ : A graph where each edge is present with probability $p$ , independent of other edges.

To create an ER network:

Go to Network > Create Random Network > Erdos-Renyi.
Specify the number of nodes ( $n$ ) and either the edge probability ( $p$ ) or the number of edges ( $M$ ).
Choose whether the network is directed, undirected, or allows self-loops.

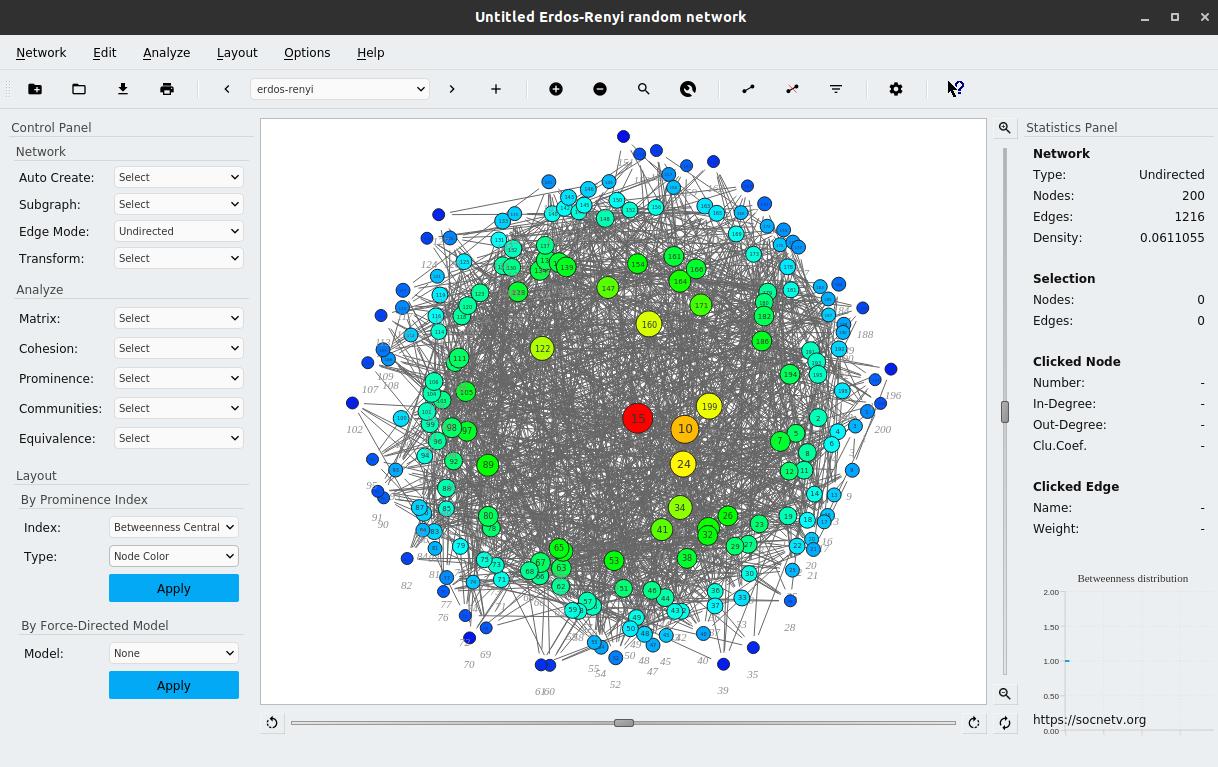Erdos-Renyi random network

Lattice Networks

SocNetV can generate regular lattice networks with arbitrary dimensions $d$ , size $l$ for each dimension, and custom neighborhood size $n$ , which defines the distance within which neighbors are connected.

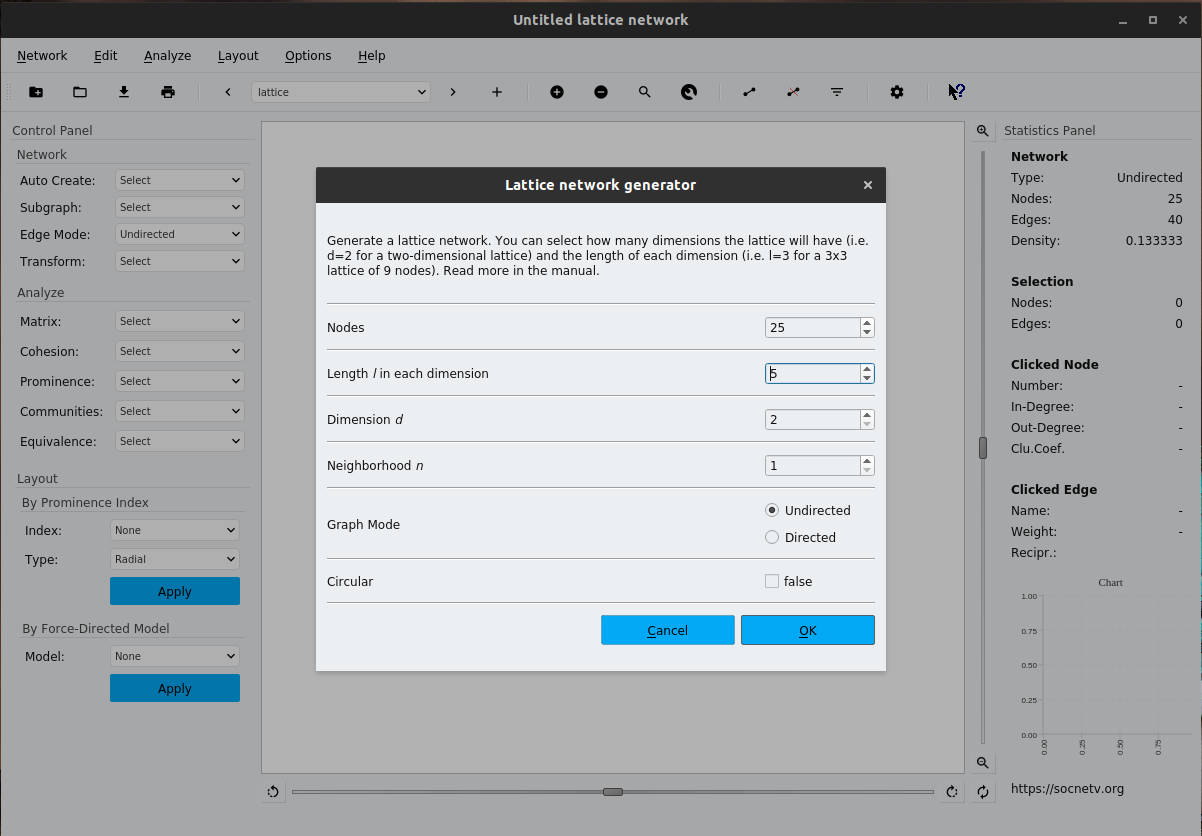The lattice generator

Ring Lattices

Ring lattices are a type of network where nodes are arranged in a ring, each connected to $d/2$ neighbors on either side. For example, in a 4-lattice of 10 nodes, node 6 connects to nodes 4, 5, 7, and 8.

To create a ring lattice network, go to Network > Create Random Network > Ring Lattice, then specify the number of nodes and degree $d$ .

Web Crawler: Networks of Webpages

SocNetV includes a web crawler that creates networks of linked webpages. Starting from an initial URL, the crawler:

Downloads the HTML of the page.
Extracts all links (href) to other pages (internal or external).
Adds these links as nodes and edges in the resulting network.

To use the web crawler:

Go to Network > Web Crawler or press Shift+C. The web crawler dialog will appear.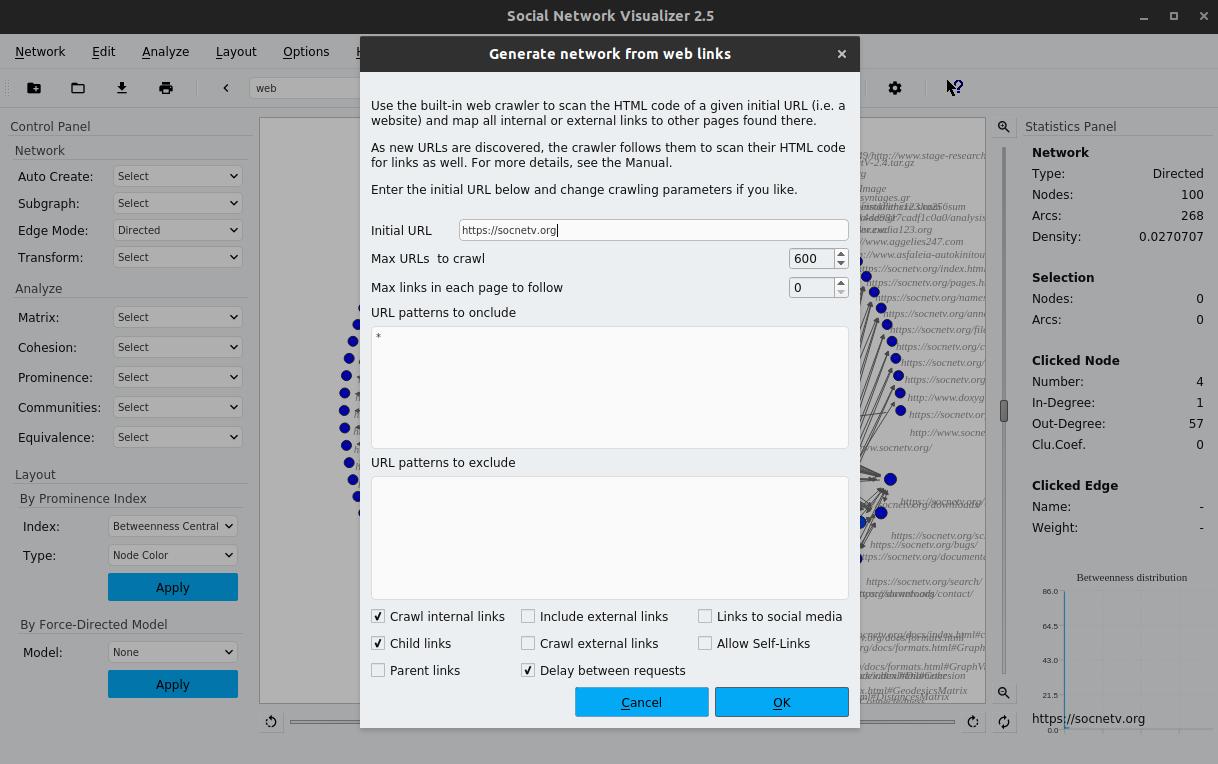 Web Crawler dialog
Enter the initial URL and configure limits, such as:
- Maximum URLs to crawl (total nodes in the network).
- Maximum links per page to consider.
Specify patterns to include or exclude and the type of links to follow (internal, external, or both). Add delays between requests to prevent overloading servers.
Press “OK” to begin crawling.

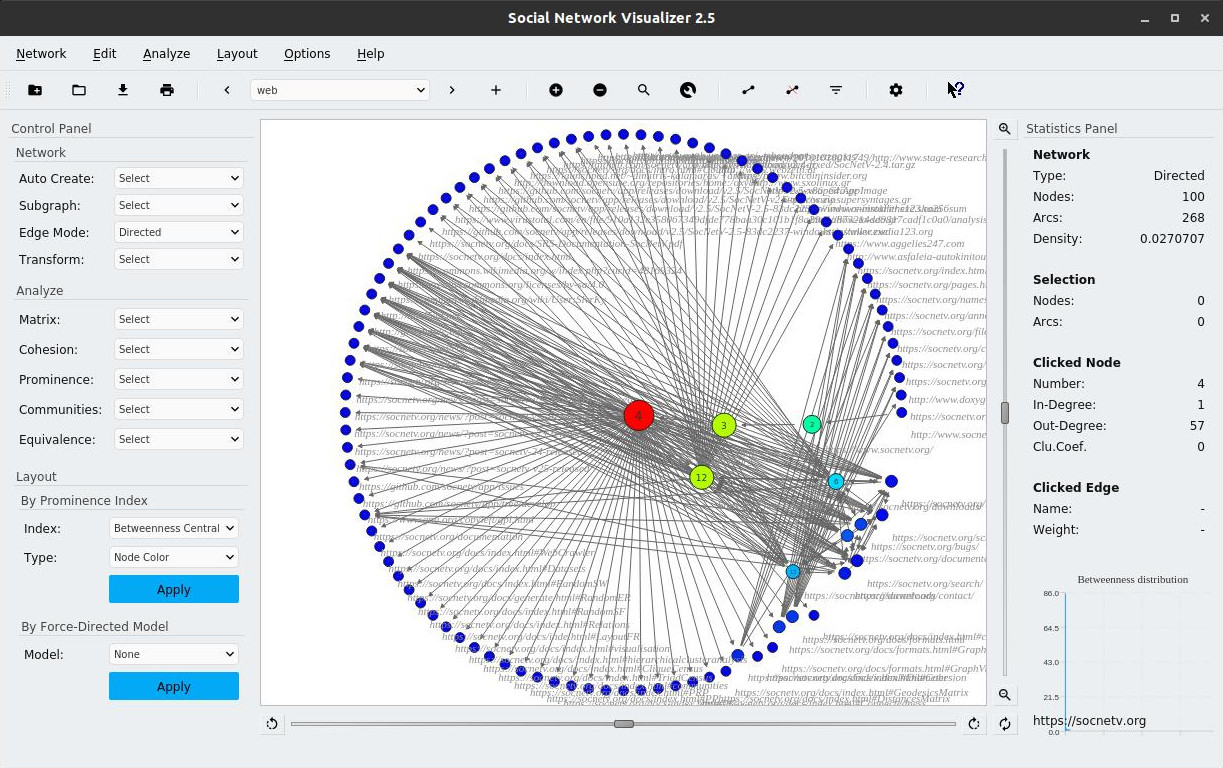Network generated by the Web Crawler